Signal-to-Noise Ratio
After reading this section you will be able to do the following:
- Define signal-to-noise ratio.
- Explane the role signal-to-noise ratio plays in defect detectability.
In a previous page, the effect that frequency and wavelength have on flaw detectability was discussed. However, the detection of a defect involves many factors other than the relationship of wavelength and flaw size. For example, the amount of the wave that reflects from a defect is also dependent on the impedance mismatch between the flaw and the surrounding material. A void is generally a better reflector than a metallic inclusion because the impedance mismatch is greater between air and metal than between two metals.
Often, the surrounding material has competing reflections. Microstructure grains in metals and the aggregate of concrete are a couple of examples. A good measure of detectability of a flaw is its signal-to-noise ratio (S/N). The signal-to-noise ratio is a measure of how the signal from the defect compares to other background reflections (categorized as "noise"). A signal-to-noise ratio of 3 to 1 is often required as a minimum. The absolute noise level and the absolute strength of an echo from a "small" defect depends on a number of factors, which include:
- The probe size and focal properties.
- The probe frequency, bandwidth and efficiency.
- The inspection path and distance (water and/or solid).
- The interface (surface curvature and roughness).
- The flaw location with respect to the incident beam.
- The inherent noisiness of the metal microstructure.
- The inherent reflectivity of the flaw, which is dependent on its acoustic impedance, size, shape, and orientation.
- Cracks and volumetric defects can reflect ultrasonic waves quite differently. Many cracks are "invisible" from one direction and strong reflectors from another.
- Multifaceted flaws will tend to scatter sound away from the transducer.
The following formula relates some of the variables affecting the signal-to-noise ratio (S/N) of a defect:
Where is the speed of sound in the metal, wx and wy are the lateral beam widths at the flaw depth, is the pulse duration, Aflow(f0) is the flaw scattering amplitude at center frequency, and FOM(f0) is the noise Figure of Merit at center frequency.
Rather than go into the details of this formulation, a few fundamental relationships can be pointed out. The signal-to-noise ratio (S/N), and therefore, the detectability of a defect:
- Increases with increasing flaw size (scattering amplitude). The detectability of a defect is directly proportional to its size.
- Increases with a more focused beam. In other words, flaw detectability is inversely proportional to the transducer beam width.
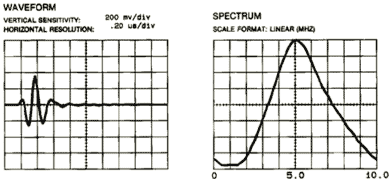
- Increases with decreasing pulse width (delta-t). In other words, flaw detectability is inversely proportional to the duration of the pulse produced by an ultrasonic transducer. The shorter the pulse (often higher frequency), the better the detection of the defect. Shorter pulses correspond to broader bandwidth frequency response. See the figure below showing the waveform of a transducer and its corresponding frequency spectrum.
- Decreases in materials with high density and/or a high ultrasonic velocity. The signal-to-noise ratio (S/N) is inversely proportional to material density and acoustic velocity.
- Generally increases with frequency. However, in some materials, such as titanium alloys, both the "Aflaw" and the "Figure of Merit (FOM)" terms in the equation change at about the same rate with changing frequency. So, in some cases, the signal-to-noise ratio (S/N) can be somewhat independent of frequency.
Review:
- The signal-to-noise ratio is a measure of how the signal from the defect compares to other background reflections (categorized as "noise").
- A signal-to-noise ratio of 3 to 1 is often required as a minimum to detect a flaw.