Refraction and Snell's Law
After reading this section you will be able to the following:
- Describe what refraction and reflection is.
- Explain Snell's Law.
 When an ultrasonic or EM wave passes through an interface between two materials at an oblique angle, and the materials have different indices of refraction, both reflected and refracted waves are produced. This also occurs with light, which is why objects seen across an interface appear to be shifted relative to where they really are. For example, if you look straight down at an object at the bottom of a glass of water, it looks closer than it really is. A good way to visualize how light and sound refract is to shine a flashlight into a bowl of slightly cloudy water noting the refraction angle with respect to the incident angle.
When an ultrasonic or EM wave passes through an interface between two materials at an oblique angle, and the materials have different indices of refraction, both reflected and refracted waves are produced. This also occurs with light, which is why objects seen across an interface appear to be shifted relative to where they really are. For example, if you look straight down at an object at the bottom of a glass of water, it looks closer than it really is. A good way to visualize how light and sound refract is to shine a flashlight into a bowl of slightly cloudy water noting the refraction angle with respect to the incident angle.
Refraction takes place at an interface due to the different velocities of the waves within the two materials. The velocity of the wave in each material is determined by the material properties (elastic modulus, density, dielectric properties, refractive index) for that material. In the animation below, a series of plane waves are shown traveling in one material and entering a second material that has a higher wave speed. Therefore, when the wave encounters the interface between these two materials, the portion of the wave in the second material is moving faster than the portion of the wave in the first material. It can be seen that this causes the wave to bend.
Snell's Law describes the relationship between the angles and the velocities of the waves. Snell's law equates the ratio of material velocities V1 and V2 to the ratio of the sine's of incident (Q1) and refracted (Q2) angles, as shown in the following equation.
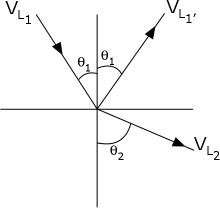 |
Where: VL1 is the longitudinal wave velocity in material 1. VL2 is the longitudinal wave velocity in material 2. |
Note that in the diagram above, there is a reflected longitudinal wave (VL1' ) shown. This wave is reflected at the same angle as the incident wave because the two waves are traveling in the same material, and hence have the same velocities. This reflected wave is unimportant in our explanation of Snell's Law, but it should be remembered that some of the wave energy is reflected at the interface. In the applet below, only the incident and refracted waves are shown. The angle of either wave can be adjusted by clicking and dragging the mouse in the region of the arrows. Values for the angles or wave velocities can also be entered in the dialog boxes so the that applet can be used as a Snell's Law calculator.
When a wave moves from a slower to a faster material, there is an incident angle that makes the angle of refraction for the wave 90o. This is know as the first critical angle. The first critical angle can be found from Snell's law by putting in an angle of 90° for the angle of the refracted ray. In the case of acoustic waves, at the critical angle of incidence much of the acoustic energy is in the form of an inhomogeneous compression wave, which travels along the interface and decays exponentially with depth from the interface. This wave is sometimes referred to as a "creep wave." Because of their inhomogeneous nature and the fact that they decay rapidly, creep waves are not used as extensively as Rayleigh surface waves in NDT. However, creep waves are sometimes more useful than Rayleigh waves because they suffer less from surface irregularities and coarse material microstructure due to their longer wavelengths.
Review:
- Refraction is a change in direction of a wave due to a change in its speed, which occurs due to material differences.
- Snell's Law describes the relationship between the angles and the velocities of the waves.