Reflection and Transmission Coefficients
After reading this section you will be able to do the following:
- Understand how reflection and transmission varies based on materials.
- Calculate reflection and transmission coefficients.
Waves are reflected at boundaries where there is a difference in impedances (Z) of the materials on each side of the boundary. This difference in Z is commonly referred to as the impedance mismatch. The greater the impedance mismatch, the greater the percentage of energy that will be reflected at the interface or boundary between one medium and another.
The fraction of the incident wave intensity that is reflected can be derived because particle velocity and local particle pressures must be continuous across the boundary. When the impedances of the materials on both sides of the boundary are known, the fraction of the incident wave intensity that is reflected can be calculated with the equations below. The values produced are known as reflection coefficients. Reflection coefficients can be in terms of amplitude or in terms of energy. The reflection coefficient is the fraction of incident energy or amplitude that is reflected as the incident wave reaches the boundary. Unlike energy reflection coefficients, amplitude reflection coefficients depend on what kind of quantity you are using to represent the wave amplitude and whether that quantity corresponds to the numerator or denominator of the impedance. The amplitude reflection coefficient for force, stress, voltage, or electric field waves is
The amplitude reflection coefficient for displacement, velocity, current, or magnetic field waves is
The energy reflection coefficient does not depend on the type of wave and is
Transmission coefficients are likewise used to calculate the fraction of an incident wave that transmits across a boundary. For force, stress, voltage, or electric field wave representations, the amplitude transmission coefficient is
For displacement, velocity, current, or magnetic field wave representations, the amplitude transmission coefficient is
Interestingly, the amplitude reflection and transmission coefficients do not in general add up to 1.0 because amplitude is not conserved across the boundary. In contrast, since the amount of reflected energy plus the transmitted energy must equal the total amount of incident energy, the energy transmission coefficient is calculated by simply subtracting the reflection coefficient from one
Formulations for energy reflection and transmission coefficients for elastic (mechanical) waves are shown in the interactive applet below. Different materials may be selected or the material velocity and density may be altered to change the acoustic impedance of one or both materials. The red arrow represents reflected sound and the blue arrow represents transmitted sound.
Note that the reflection and transmission coefficients are often expressed in decibels (dB) to allow for large changes in signal strength to be more easily compared.
Using the applet above, note that the energy reflected at a water-stainless steel interface is 0.88 or 88%. The amount of energy transmitted into the second material is 0.12 or 12%. The amount of reflection and transmission energy in dB terms are -1.1 dB and -18.2 dB respectively. The negative sign indicates that individually, the amount of reflected and transmitted energy is smaller than the incident energy.
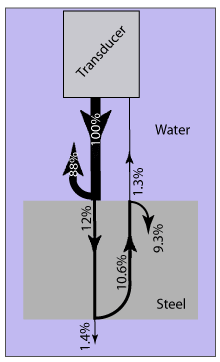 If reflection and transmission at interfaces is followed through the component, only a small percentage of the original energy makes it back to the transducer, even when loss by attenuation is ignored. For example, consider an immersion inspection of a steel block, like the one on the left. The sound energy leaves the transducer, travels through the water, encounters the front surface of the steel, encounters the back surface of the steel and reflects back through the front surface on its way back to the transducer. At the water steel interface (front surface), 12% of the energy is transmitted. At the back surface, 88% of the 12% that made it through the front surface is reflected. This is 10.6% of the intensity of the initial incident wave. As the wave exits the part back through the front surface, only 12% of 10.6 or 1.3% of the original energy is transmitted back to the transducer.
If reflection and transmission at interfaces is followed through the component, only a small percentage of the original energy makes it back to the transducer, even when loss by attenuation is ignored. For example, consider an immersion inspection of a steel block, like the one on the left. The sound energy leaves the transducer, travels through the water, encounters the front surface of the steel, encounters the back surface of the steel and reflects back through the front surface on its way back to the transducer. At the water steel interface (front surface), 12% of the energy is transmitted. At the back surface, 88% of the 12% that made it through the front surface is reflected. This is 10.6% of the intensity of the initial incident wave. As the wave exits the part back through the front surface, only 12% of 10.6 or 1.3% of the original energy is transmitted back to the transducer.
Review:
- Waves are reflected at boundaries where there is a difference in impedances (Z) of the materials on each side of the boundary.
- Reflection and transmission coefficients are often expressed in dB.