Mode Conversion
After reading this section you will be able to do the following:
- Explain what mode conversion is and what causes it.
When a wave travels in a solid material, one form of wave energy can be transformed into another form. For example, when a longitudinal waves hits an interface at an angle, some of the energy can cause particle movement in the transverse direction to start a shear (transverse) wave. Mode conversion occurs when a wave encounters an interface between materials of different impedances and the incident angle is not normal to the interface. From the ray tracing clip below, it can be seen that since mode conversion occurs every time a wave encounters an interface at an angle, signals can become confusing at times.

In the previous sections, it was pointed out that when waves pass through an interface between materials having different wave speeds, refraction takes place at the interface. The larger the difference in wave speeds between the two materials, the more the wave is refracted. Notice that the shear wave is not refracted as much as the longitudinal wave. This occurs because shear waves travel slower than longitudinal waves. Therefore, the velocity difference between the incident longitudinal wave and the shear wave is not as great as it is between the incident and refracted longitudinal waves. Also note that when a longitudinal wave is reflected inside the material, the reflected shear wave is reflected at a smaller angle than the reflected longitudinal wave. This is also due to the fact that the shear velocity is less than the longitudinal velocity within a given material.
Snell's Law holds true for shear waves as well as longitudinal waves and can be written as follows.
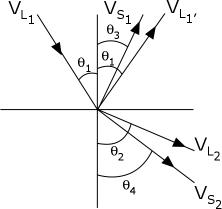
Where:
VL1 is the longitudinal wave velocity in material 1.
VL2 is the longitudinal wave velocity in material 2.
VS1 is the shear wave velocity in material 1.
VS2 is the shear wave velocity in material 2.
In the applet below, the shear (transverse) wave ray path has been added. The ray paths of the waves can be adjusted by clicking and dragging in the vicinity of the arrows. Values for the angles or the wave velocities can also be entered into the dialog boxes. It can be seen from the applet that when a wave moves from a slower to a faster material, there is an incident angle which makes the angle of refraction for the longitudinal wave 90 degrees. As mentioned on the previous page, this is known as the first critical angle and all of the energy from the refracted longitudinal wave is now converted to a surface following longitudinal wave. This surface following wave is sometime referred to as a creep wave and it is not very useful in NDT because it dampens out very rapidly.
Beyond the first critical angle, only the shear wave propagates into the material. For this reason, most angle beam transducers use a shear wave so that the signal is not complicated by having two waves present. In many cases there is also an incident angle that makes the angle of refraction for the shear wave 90 degrees. This is known as the second critical angle and at this point, all of the wave energy is reflected or refracted into a surface following shear wave or shear creep wave. Slightly beyond the second critical angle, surface waves will be generated.
Note that the applet defaults to compressional velocity in the second material. The refracted compressional wave angle will be generated for given materials and angles. To find the angle of incidence required to generate a shear wave at a given angle complete the following:
- Set V1 to the longitudinal wave velocity of material 1. This material could be the transducer wedge or the immersion liquid.
- Set V2 to the shear wave velocity (approximately one-half its compressional velocity) of the material to be inspected.
- Set Q2 to the desired shear wave angle.
- Read Q1, the correct angle of incidence.
Review:
- When a wave travels in a solid material, one form of wave energy can be transformed into another form.
- When a wave moves from a slower to a faster material, there is an incident angle which makes the angle of refraction for the longitudinal wave 90 degrees. This is the critical angle.