Wave Number and Impedance

After reading this section you will be able to do the following:

  • Describe different wave parameters that are related to the material the wave is in.

Refractive Index

Refractive index is a material property that determines how much light (or a wave at other frequencies) is bent and how much is reflected/transmitted when it travels from one material to another. The refractive index is related to the complex dielectric constant by the following equation:

n = ϵ r n={\sqrt{\epsilon_r}}

As a reminder:

ϵ = ϵ r ϵ o \epsilon={\epsilon_r \epsilon_o}

μ = μ r μ o \mu={\mu_r \mu_o} 

Wave Speed and Speed of Light

In free space an EM waves travels at the speed of light, which is approximately 3x10^8 m/s. In a material, an EM wave travels more slowly as a function of the dielectric constant of the material. In general, the wave speed (vp) is related to the permeability and the permittivity by the following equation:

v p = 1 μ ϵ v_p={1 \over \sqrt{\mu \epsilon}}

When the wave is traveling in free space this equation works out such that vp equals the speed of light. You can test this yourself by plugging in the following values:

μ = μ o μ r = ( 4 π × 10 − 7 ) ( 1 ) = 4 π × 10 − 7 H / m \mu={\mu_o \mu_r} ={(4\pi \times 10^{-7})(1)}={4\pi \times 10^{-7}} H/m

ϵ = ϵ o ϵ r = ( 8.854 × 10 − 12 ) ( 1 ) = 8.854 × 10 − 12 F / m \epsilon={\epsilon_o \epsilon_r} ={(8.854 \times 10^{-12})(1)}={8.854 \times 10^{-12}} F/m

You should get close to 3x10^8 m/s!

Wavenumber

The wavenumber, also called the propagation number or propagation constant, can be thought of as a spatial frequency - how many wavelengths occur per unit distance. In free space it is the ratio of the angular frequency to the speed of light and in a material it is related to the refractive index. 

Intrinsic Impedance

The intrinsic impedance is the impedance an EM wave faces as it travels through a medium. When the medium is homogeneous and the EM wave is a transverse electromagnetic (TEM) wave, then the intrinsic impedance is equal to the wave impedance. A TEM wave is simply a special case of EM waves where the linked electric fields and magnetic fields that make up the wave are orthogonal to each other and to the direction that the wave is traveling in. A visualization of a TEM wave is shown below. 

 

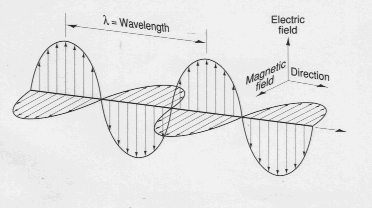
When the wave is traveling in a dielectric then the intrinsic impedance (represented by the Greek letter eta) can be described with the following equation:

η = μ ϵ \eta={\sqrt{\mu \over\epsilon}}

The equation above shows that the intrinsic impedance is related to the permeability and the permittivity of the material. 

Review:

  1. Refractive index, wave speed, wave number, and intrinsic impedance are all interrelated quantities. 
  2. Chaning the material properties changes how a wave will propagate through that material.