Stress and Strain
Stress
The term stress (σ) is used to express the loading in terms of force applied to a certain cross-sectional area of an object. From the perspective of loading, stress is the applied force or system of forces that tends to deform a body. From the perspective of what is happening within a material, stress is the internal distribution of forces within a body that balance and react to the loads applied to it. The stress distribution may or may not be uniform, depending on the nature of the loading condition. For example, a bar loaded in pure tension will essentially have a uniform tensile stress distribution. However, a bar loaded in bending will have a stress distribution that changes with distance perpendicular to the normal axis.
Simplifying assumptions are often used to represent stress as a vector quantity for many engineering calculations and for material property determination. The word "vector" typically refers to a quantity that has a "magnitude" and a "direction". For example, the stress in an axially loaded bar is simply equal to the applied force divided by the bar's cross-sectional area.
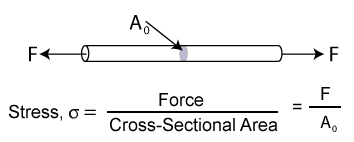
Some common measurements of stress are:
Psi = lbs/in2 (pounds per square inch)
ksi or kpsi = kilopounds/in2 (one thousand or 103 pounds per square inch)
Pa = N/m 2 (Pascals or Newtons per square meter)
kPa = Kilopascals (one thousand or 103 Newtons per square meter)
GPa = Gigapascals (one million or 106 Newtons per square meter)
*Any metric prefix can be added in front of psi or Pa to indicate the multiplication factor
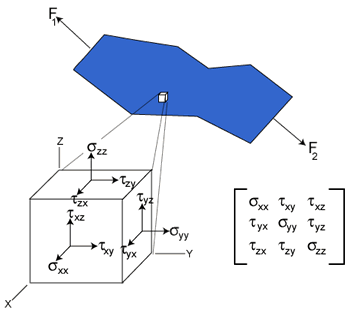 It must be noted that the stresses in most 2-D or 3-D solids are actually more complex and need be defined more methodically. The internal force acting on a small area of a plane can be resolved into three components: one normal to the plane and two parallel to the plane. The normal force component divided by the area gives the normal stress (σ), and parallel force components divided by the area give the shear stress (τ). These stresses are average stresses as the area is finite, but when the area is allowed to approach zero, the stresses become stresses at a point. Since stresses are defined in relation to the plane that passes through the point under consideration, and the number of such planes is infinite, there appear an infinite set of stresses at a point. Fortunately, it can be proven that the stresses on any plane can be computed from the stresses on three orthogonal planes passing through the point. As each plane has three stresses, the stress tensor has nine stress components, which completely describe the state of stress at a point.
It must be noted that the stresses in most 2-D or 3-D solids are actually more complex and need be defined more methodically. The internal force acting on a small area of a plane can be resolved into three components: one normal to the plane and two parallel to the plane. The normal force component divided by the area gives the normal stress (σ), and parallel force components divided by the area give the shear stress (τ). These stresses are average stresses as the area is finite, but when the area is allowed to approach zero, the stresses become stresses at a point. Since stresses are defined in relation to the plane that passes through the point under consideration, and the number of such planes is infinite, there appear an infinite set of stresses at a point. Fortunately, it can be proven that the stresses on any plane can be computed from the stresses on three orthogonal planes passing through the point. As each plane has three stresses, the stress tensor has nine stress components, which completely describe the state of stress at a point.
Strain
Strain is the response of a system to an applied stress. When a material is loaded with a force, it produces a stress, which then causes a material to deform. Engineering strain is defined as the amount of deformation in the direction of the applied force divided by the initial length of the material. This results in a unitless number, although it is often left in the unsimplified form, such as inches per inch or meters per meter. For example, the strain in a bar that is being stretched in tension is the amount of elongation or change in length divided by its original length. As in the case of stress, the strain distribution may or may not be uniform in a complex structural element, depending on the nature of the loading condition.
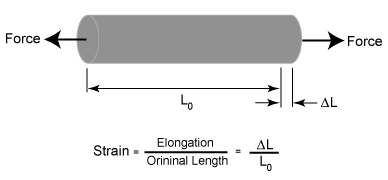
If the stress is small, the material may only strain a small amount and the material will return to its original size after the stress is released. This is called elastic deformation, because like elastic it returns to its unstressed state. Elastic deformation only occurs in a material when stresses are lower than a critical stress called the yield strength. If a material is loaded beyond it elastic limit, the material will remain in a deformed condition after the load is removed. This is called plastic deformation.
Engineering and True Stress and Strain
The discussion above focused on engineering stress and strain, which use the fixed, undeformed cross-sectional area in the calculations. True stress and strain measures account for changes in cross-sectional area by using the instantaneous values for the area. The engineering stress-strain curve does not give a true indication of the deformation characteristics of a metal because it is based entirely on the original dimensions of the specimen, and these dimensions change continuously during the testing used to generate the data.
Engineering stress and strain data is commonly used because it is easier to generate the data and the tensile properties are adequate for engineering calculations. When considering the stress-strain curves in the next section, however, it should be understood that metals and other materials continues to strain-harden until they fracture and the stress required to produce further deformation also increase.
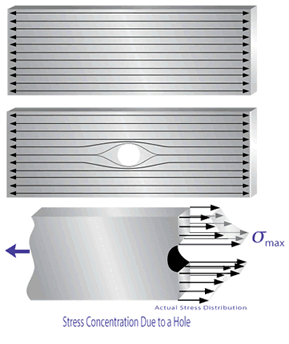 Stress Concentration
Stress Concentration
When an axial load is applied to a piece of material with a uniform cross-section, the norm al stress will be uniformly distributed over the cross-section. However, if a hole is drilled in the material, the stress distribution will no longer be uniform. Since the material that has been removed from the hole is no longer available to carry any load, the load must be redistributed over the remaining material. It is not redistributed evenly over the entire remaining cross-sectional area but instead will be redistributed in an uneven pattern that is highest at the edges of the hole as shown in the image. This phenomenon is known as stress concentration.