Depth of Penetration and Current Density
After reading this section you will be able to do the following:
- Define what the skin effect is and how it describes current and radiation penetration into materials.
Eddy currents are closed loops of induced current circulating in planes perpendicular to the magnetic flux. They normally travel parallel to the coil's winding and flow is limited to the area of the inducing magnetic field. Eddy currents concentrate near the surface adjacent to an excitation coil and their strength decreases with distance from the coil as shown in the image. Eddy current density decreases exponentially with depth. This phenomenon is known as the skin effect. The figures below show two eddy current simulations and show how the density of eddy currents decrease with depth. They show the in-phase components perpendicular to the material cross section with the image on the left having no directionality and the image on the right indicating directionality.

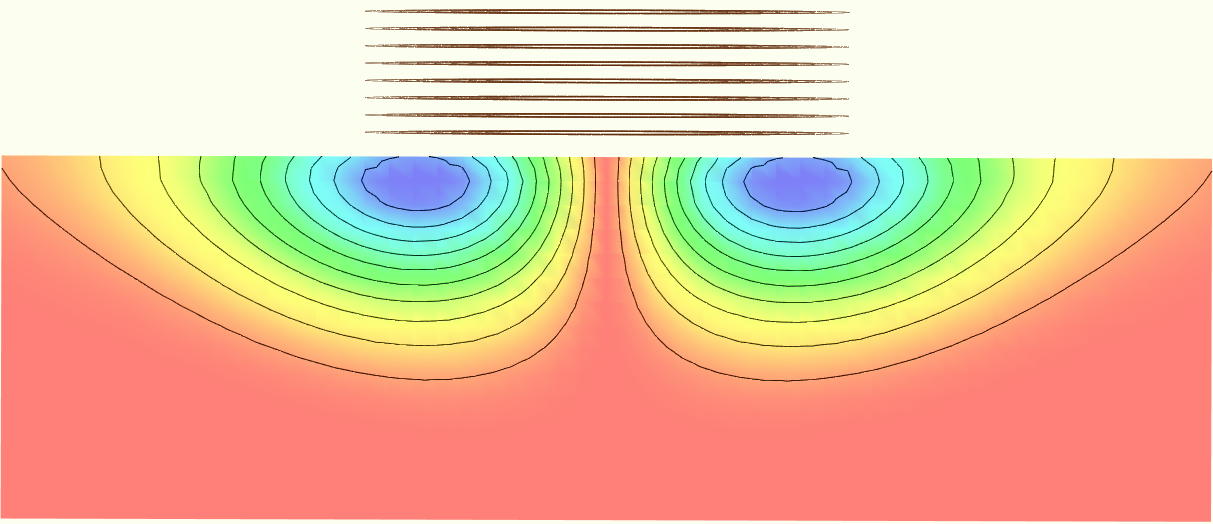
The skin effect arises when the eddy currents flowing in the test object at any depth produce magnetic fields which oppose the primary field, thus reducing the net magnetic flux and causing a decrease in current flow as the depth increases. Alternatively, eddy currents near the surface can be viewed as shielding the coil's magnetic field, thereby weakening the magnetic field at greater depths and reducing induced currents.
The depth that eddy currents and EM waves penetrate into a material is affected by the frequency of the excitation current and the electrical conductivity and magnetic permeability of the specimen. The depth of penetration decreases with increasing frequency and increasing conductivity and magnetic permeability. The depth at which eddy current density has decreased to 1/e, or about 37% of the surface density, is called the standard depth of penetration (d). The word 'standard' denotes plane wave electromagnetic field excitation within the test sample (conditions which are rarely achieved in practice). Although eddy currents penetrate deeper than one standard depth of penetration, they decrease rapidly with depth. At two standard depths of penetration (2d), eddy current density has decreased to 1/e squared or 13.5% of the surface density. At three depths (3d), the eddy current density is down to only 5% of the surface density.
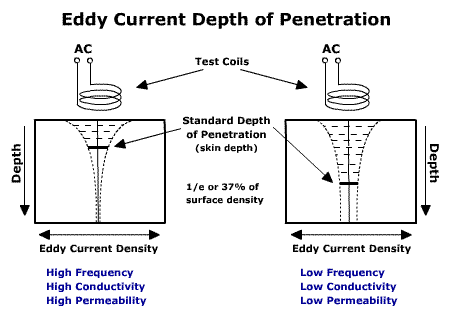
Since the sensitivity of an eddy current inspection depends on the eddy current density at the defect location, it is important to know the strength of the eddy currents at this location. When attempting to locate flaws, a frequency is often selected which places the expected flaw depth within one standard depth of penetration. This helps to assure that the strength of the eddy currents will be sufficient to produce a flaw indication. Alternately, when using eddy currents to measure the electrical conductivity of a material, the frequency is often set so that it produces three standard depths of penetration within the material. This helps to assure that the eddy currents will be so weak at the back side of the material that changes in the material thickness will not affect the eddy current measurements.
The applet below illustrates how eddy current density changes in a semi-infinite conductor. The applet can be used to calculate the standard depth of penetration. The equation for this calculation is:
Where:
δ = Standard Depth of Penetration (m)
f = Test Frequency (Hz)
μ = Magnetic Permeability (H/m)
σ = Electrical Conductivity (S/m)
(Note: The applet has an input box for relative permeability since this is often the more readily available value. The applet multiplies the relative permeability of the material by the permeability of free space to get to H/m units.)
The applet also indicates graphically the phase lag at one and two standard depths of penetration. Phase lag will be discussed on the following page.
Review:
- The depth that eddy currents and EM waves penetrate into a material is affected by the frequency of the excitation current and the electrical conductivity and magnetic permeability of the specimen