Ultrasonic Inspection Formulas

Wave Velocity

Longitudinal Wave Velocity:

V L = E ( 1 − ν ) ρ ( 1 + ν ) ( 1 − 2 ν ) V_{L}=\sqrt{\frac{E(1-\nu)}{\rho(1+\nu)(1-2\nu)}}

Where:

VL = Longitudinal Wave Velocity

E = Modulus of Elasticity

ρ = Density

ν = Poisson's Ratio

Shear Wave Velocity:

V S = E 2 ρ ( 1 + ν ) V_{S}=\sqrt{\frac{E}{2\rho(1+\nu)}}

or

V S = G ρ V_{S}=\sqrt{\frac{G}{\rho}}

Where:

VS= Shear Wave Velocity

E = Modulus of Elasticity

ρ = Density

ν = Poisson's Ratio

G = Shear Modulus

Wavelength

λ = V f \lambda=\frac{V}{f}

Where:

λ = Wavelength

V = Velocity

f = Frequency

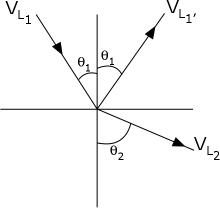
Refraction (Snell's Law)

sin ⁡ θ 1 sin ⁡ θ 2 = V 1 V 2 \frac{\sin\theta_{1}}{\sin\theta_{2}}=\frac{V_{1}}{V_{2}}

Where:

θ1 = Angle of the Incident Wave

θ2 = Angle of the Reflected Wave

V1 = Velocity of Incident Wave

V2 = Velocity of Reflected Wave

Snell's Law is used regularly when performing angle beam inspections. Snell's Law describes the relationship between the incident and refracted angles of a wave as it moves from one material into another material which has a different wave velocity. Refraction takes place at the interface due to the different velocities of the acoustic waves within the two materials. Snell's Law equates the ratio of material velocities V1 and V2 to the ratio of the sine's of incident (θ1) and refracted (θ2) angles. Snell's Law is usually presented in the form of one of the following equations.

After hitting an interface, the incident waves splits into a reflected wave and a transmitted wave.

sin ⁡ θ 1 V 1 = sin ⁡ θ 2 V 2 \frac{\sin\theta_{1}}{V_{1}}=\frac{\sin\theta_{2}}{V_{2}}

or

sin ⁡ θ 1 sin ⁡ θ 2 = V 1 V 2 \frac{\sin\theta_{1}}{\sin\theta_{2}}=\frac{V_{1}}{V_{2}}

The first equation states that the ratio of the sine of the incident angle and the wave velocity in material 1 is equal to the ratio of the sine of the refracted angle and the wave velocity in material 2. The second equation states that the ratios of the sine's of the two angles is equal to the ratio of the two velocities. It should be evident that the two equations are equivalent.

Example Calculations

Example 1

What is the incident angle that will produce a 70 degree refracted shear wave in steel using a Lucite wedge. First establish the values.

  • θ1 = the value to be determined
  • θ2 = 70o
  • V1 = 0.106 in/μs (sound velocity of a longitudinal wave in Lucite)
  • V2 = 0.128 in/μs (sound velocity of a shear wave in steel)
Plug the known values into the equation.

sin ⁡ θ 1 sin ⁡ θ 2 = V 1 V 2 \frac{\sin\theta_{1}}{\sin\theta_{2}}=\frac{V_{1}}{V_{2}}

becomes

sin ⁡ θ 1 sin ⁡ ( 70 ) = 0.106  in/μs 0.128  in/μs \frac{\sin\theta_{1}}{\sin(70)}=\frac{0.106 \text{ in/μs}}{0.128\text{ in/μs}}

Simplify by dividing the right side of the equation and determine the sine of 70 with a calculator.

sin ⁡ θ 1 0.940 = 0.828 \frac{\sin\theta_{1}}{0.940}=0.828

Multiply both sides of the equation by 0.940 to solve for Sinθ1.

0.940 × sin ⁡ θ 1 0.940 = 0.828 × 0.940 \bcancel{0.940}\times\frac{\sin\theta_{1}}{\bcancel{0.940}}=0.828\times0.940

sin ⁡ θ 1 = 0.778 \sin\theta_{1}=0.778

Finally, take the inverse sine of 0.778 to determine the angle whose sine equal 0.778.

θ 1 = 51.1 o \boxed{\theta_{1}=51.1^{o}}

Example 2

If the incident angle is 24 degrees when setting up an immersion inspection, what is the refracted shear wave angle in aluminum?

sin ⁡ θ 1 V 1 = sin ⁡ θ 2 V 2 \frac{\sin\theta_{1}}{V_{1}}=\frac{\sin\theta_{2}}{V_{2}}

First establish the values.

  • θ1 = 24o
  • θ2 = the value to be determined
  • V1 = 0.148 cm/μs (sound velocity of a longitudinal wave in Lucite)
  • V2 = 0.313 cm/μs (sound velocity of a shear wave in steel)
Plug the known values into the equation.

sin ⁡ ( 24 ) 0.148  cm/μs = sin ⁡ θ 2 0.313  cm/μs \frac{\sin(24)}{0.148\text{ cm/μs}}=\frac{\sin\theta_{2}}{0.313\text{ cm/μs}}

Determine the sine of 24 degrees with a calculator. Sin(24) = 0.407. Plug in this value and cross multiply and divide.

( 0.407 ) ( 0.313  cm/μs ) 0.148  cm/μs = sin ⁡ θ 2 \frac{(0.407)(0.313\text{ cm/μs})}{0.148\text{ cm/μs}}=\sin\theta_{2}

0.861 = sin ⁡ θ 2 0.861=\sin\theta_{2}

Finally, take the inverse sine of 0.861 to determine the angle whose sine equal 0.861.

θ 2 = 59.4 o \boxed{\theta_{2}=59.4^{o}}

Acoustic Impedance

Z = ρ V Z=\rho V

Where:

Z = Acoustic Impedance

ρ = Density

V = Velocity

Learn more about acoustic impedance in the physics section.

Reflection

R = ( Z 2 − Z 1 Z 2 + Z 1 ) 2 R=\left(\frac{Z_{2}-Z_{1}}{Z_{2}+Z_{1}}\right)^{2}

Where:

R = Energy Reflection Coefficient

Z1 = Acoustic Impedance of Medium 1

Z2 = Acoustic Impedance of Medium 2

Learn more about reflection and transmission of energy in the physics of waves section.

Near Field

N = D 2 4 λ N=\frac{D^{2}}{4\lambda}

or

N = D 2 f 4 V N=\frac{D^{2}f}{4V}

Where:

N = Near Field

D = Transducer Diameter

λ = Wavelength

f = Frequency

V = Velocity

Near the ultrasonic transducer there are significant fluctuations in the sound intensity due to constructive and destructive interference of the multiple waves which originate from the transducer face. Because of acoustic variations within this field, called the near field, it can be extremely difficult to accurately evaluate flaws in materials when they are positioned within this area.

However, at some point the pressure waves combine to form a relatively uniform front. The area where the ultrasonic beam is more uniform and spreads out in a pattern originating from the center of the transducer is called the far field. Knowing where the far field starts is important since optimal detection occur when flaws are located at the start of far field since this is where the sound wave is well behaved and at its maximum strength. The transition point between the near field and the far field (sometimes referred to as the "natural focus" of an unfocused transducer) can be calculated if the frequency and diameter of the transducer and the speed of sound in the material are known.

Example Calculation

Calculate the end of the near field when using a 5 MHz, 0.375 inch diameter transducer to inspect a component made of brass. The sound velocity in brass is 0.1685x106 inch/second

N = D 2 f 4 V N=\frac{D^{2}f}{4V}

Note: Sometimes the radius of the transducer is used (like in the Java calculator). When the radius is used, the four in the denominator go away because the diameter squared divided by four is equal to the radius squared.

Substitute the values into the formula.

N = ( 0.375  in ) 2 ( 5 × 10 6  cycles/sec ) 4 ( 0.1685 × 10 6  in/sec ) N=\frac{(0.375\text{ in})^{2}(5\times10^{6}\text{ cycles/sec})}{4(0.1685\times10^{6}\text{ in/sec})}

Complete the square and cancel terms where possible.

N = ( 0.375  in ) 2 ( 5 × 10 6  cycles/ sec ) 4 ( 0.1685 × 10 6  in/sec ) N=\frac{(0.375\text{ in})^{\cancel{2}}(5\cancel{\times10^{6}}\text{ cycles/}\cancel{\text{sec}})}{4(0.1685\cancel{\times10^{6}}\cancel{\text{ in/sec}})}

Multiply.

N = 0.703  in cycle 0.675 N=\frac{0.703\text{ in cycle}}{0.675}

Divide.

N = 1.04  inches N=1.04\text{ inches}

The near field will extend into the material 1.04 inch from the transducer face. Within this near field area, it is hard to predict the signal amplitude from a reflector.

Learn more about radiated fields in the ultrasonic equipment section.

Beam Spread Half-Angle

sin ⁡ θ = 1.2 λ D \sin\theta=1.2\frac{\lambda}{D}

or

sin ⁡ θ = 1.2 V D f \sin\theta=1.2\frac{V}{Df}

Where:

λ = Wavelength

D = Transducer Diameter

V = Velocity

f = Frequency

A round transducers produces a cylindrical sound field in front of the transducer. However, the energy in the beam does not remain in a cylinder, but instead spread out as it propagates through the material. The phenomenon is usually referred to as beam spread.

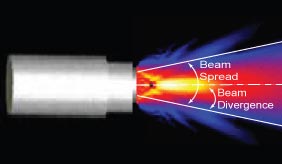
The size of the beam changes as it gets further from the transducer.

Beam spread for a flat piston source transducer is a function of the transducer diameter (D), transducer frequency (f), and the sound velocity (V) in the liquid or solid medium through which the sound is traveling. The equation below can be used to calculate the beam divergence angle (1/2 beam spread angle). This angle represents a measure from the center of the acoustic axis to the point where the sound pressure has decreased by one half (-6 dB) to the side of the acoustic axis.

Example Calculation

Calculate the beam spread when using a 2.25 MHz, 0.375 inch diameter transducer to inspect a component made of brass. The sound velocity in brass is 0.1685x106 inch/second. First, substitute the values into the formula.

sin ⁡ θ = 1.2 0.1685 × 10 6  in/sec ( 0.375  in ) ( 2.25 × 10 6  cycles/ sec ) \sin\theta=1.2\frac{0.1685\times10^{6}\text{ in/sec}}{(0.375\text{ in})(2.25\times10^{6}\text{ cycles/}\text{sec})}

Cancel terms where possible.

sin ⁡ θ = 1.2 0.1685 × 10 6  in/sec ( 0.375  in ) ( 2.25 × 10 6  cycles/ sec ) \sin\theta=1.2\frac{0.1685\cancel{\times10^{6}}\cancel{\text{ in/sec}}}{(0.375\cancel{\text{ in}})(2.25\cancel{\times10^{6}}\text{ cycles/}\cancel{\text{sec}})}

Simplify.

sin ⁡ θ = 1.2 0.1685 ( 0.375 ) ( 2.25 ) \sin\theta=1.2\frac{0.1685}{(0.375)(2.25)}

Multiply and divide.

sin ⁡ θ = 0.2396 \sin\theta=0.2396

With a calculator find the inverse sin of 0.2396.

θ = 13.86 o \theta=13.86^{o}

The beam divergency is 13.86 degrees so beam spread, which is 2 times the beam divergency, will be approximately 27.7 degrees.

Learn more about beam spread in the ultrasonic equipment section.

Decibel (dB) Gain and Loss

Δ I ( d B ) = 20 log ⁡ P 2 P 1 \Delta I(dB)=20\log\frac{P_{2}}{P_{1}}

Where:

ΔI(dB) = Difference in sound Intensity in Decibels

P1 = Pressure Amplitude 1

P2 = Pressure Amplitude 2

Calculation Examples

Example 1:

Two sound pressure measurements are made using an ultrasonic transducer. The output voltage from the transducer is 600 mV for the first measurement and 100 mV for the second measurement. Calculate the difference in the sound intensity, in dB, between the two measurements?

Δ I ( d B ) = 20 log ⁡ V 2 V 1 \Delta I(dB)=20\log\frac{V_{2}}{V_{1}}

Substitute in the voltage values:

Δ I ( d B ) = 20 log ⁡ 100  mV 600  mV \Delta I(dB)=20\log\frac{100 \text{ mV}}{600\text{ mV}}

Divide to get a decimal value for the ratio:

Δ I ( d B ) = 20 log ⁡ 0.1667 \Delta I(dB)=20\log0.1667

Take the log of 0.1667:

Δ I ( d B ) = 20 ( − 0.7782 ) \Delta I(dB)=20(-0.7782)

Multiply:

Δ I ( d B ) = − 15.56 \Delta I(dB)=-15.56

The sound intensity changed by -15.56dB. In other words, the sound intensity decreased by 15.56 dB

Example 2:

If the intensity between two ultrasonic measurements increases by 6 dB, and the first measurement produces a transducer output voltage of 30 mV, what was the transducer output voltage for the second measurement?

Δ I ( d B ) = 20 log ⁡ V 2 V 1 \Delta I(dB)=20\log\frac{V_{2}}{V_{1}}

Substitute the know information in to the equation:

6 = 20 log ⁡ V 2 30  mV 6=20\log\frac{V_{2}}{30\text{ mV}}

Divide both sides of the equation by 20

6 20 = 20 log ⁡ V 2 30  mV 20 \frac{6}{20}=\frac{\cancel{20}\log\frac{V_{2}}{30\text{ mV}}}{\cancel{20}}

Simplify:

.3 = log ⁡ V 2 30  mV .3=\log\frac{V_{2}}{30\text{ mV}}

Clear the log:

10 0.3 = V 2 30  mV 10^{0.3}=\frac{V_{2}}{30\text{ mV}}

Simplify:

∼ 2 = V 2 30  mV \sim2=\frac{V_{2}}{30\text{ mV}}

Solve for P2:

60  mV = V 2 60\text{ mV}=V_{2}

The voltage output for P2 is 60mV. Notice that a 6dB increase in sound intensity doubled the voltage output.

Example 3:

Consider the sound pressure difference between the threshold of human hearing, 0 dB, and the level of sound often produce at a rock concert, 120 dB. (Note: prolonged sound levels above 85 dB are considered harmful, while levels above 120 dB are unsafe.)

120  dB = 20 log ⁡ P 2 P 1 120\text{ dB}=20\log\frac{P_{2}}{P_{1}} where: P1 is the sound pressure of the reference level, and P2 is the sound pressure experienced at the rock concert.

Divide both sides by 20:

6 = log ⁡ P 2 P 1 6=\log\frac{P_{2}}{P_{1}}

Clear the log:

10 6 = P 2 P 1 10^{6}=\frac{P_{2}}{P_{1}}

So the sound pressure at a rock concert is 106 or one million times greater than that of the threshold of human hearing.

Learn more about the decibel in the physics of waves section.