Precision Velocity Measurements

Changes in ultrasonic wave propagation speed, along with energy losses, from interactions with a materials microstructures are often used to nondestructively gain information about a material's properties. Measurements of sound velocity and ultrasonic wave attenuation can be related to the elastic properties that can be used to characterize the texture of polycrystalline metals. These measurements enable industry to replace destructive microscopic inspections with nondestructive methods.

Of interest in velocity measurements are longitudinal wave, which propagate in gases, liquids, and solids. In solids, also of interest are transverse (shear) waves. The longitudinal velocity is independent of sample geometry when the dimensions at right angles to the beam are large compared to the beam area and wavelength. The transverse velocity is affected little by the physical dimensions of the sample.

Pulse-Echo and Pulse-Echo-Overlap Methods

Rough ultrasonic velocity measurements are as simple as measuring the time it takes for a pulse of ultrasound to travel from one transducer to another (pitch-catch) or return to the same transducer (pulse-echo). Another method is to compare the phase of the detected sound wave with a reference signal: slight changes in the transducer separation are seen as slight phase changes, from which the sound velocity can be calculated. These methods are suitable for estimating acoustic velocity to about 1 part in 100. Standard practice for measuring velocity in materials is detailed in ASTM E494.

Precision Velocity Measurements (using EMATs)

Electromagnetic-acoustic transducers (EMAT) generate ultrasound in the material being investigated. When a wire or coil is placed near to the surface of an electrically conducting object and is driven by a current at the desired ultrasonic frequency, eddy currents will be induced in a near surface region. If a static magnetic field is also present, these currents will experience Lorentz forces of the form

$$F=J\times B$$

where F is a body force per unit volume, J is the induced dynamic current density, and B is the static magnetic induction.

The most important application of EMATs has been in nondestructive evaluation (NDE) applications such as flaw detection or material property characterization. Couplant free transduction allows operation without contact at elevated temperatures and in remote locations. The coil and magnet structure can also be designed to excite complex wave patterns and polarizations that would be difficult to realize with fluid coupled piezoelectric probes. In the inference of material properties from precise velocity or attenuation measurements, use of EMATs can eliminate errors associated with couplant variation, particularly in contact measurements.

Differential velocity is measured using a T1-T2---R fixed array of EMAT transducers at 0, 45°, 90° or 0°, 90° relative rotational directions depending on device configuration:

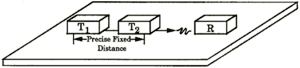
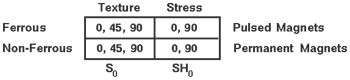
EMAT Driver Frequency: 450-600 KHz (nominal)
Sampling Period: 100 ns
Time Measurement Accuracy:

• Resolution 0.1 ns
• Accuracy required for less than 2 KSI Stress Measurements: Variance 2.47 ns
• Accuracy required for texture: Variance 10.0 Ns
  • W440 < 3.72E-5
  • W420 < 1.47E-4
  • W400 < 2.38E-4

Time Measurement Technique

Fourier Transform-Phase-Slope determination of delta time between received RF bursts (T2-R) - (T1-R), where T2 and T1 EMATs are driven in series to eliminate differential phase shift due to probe liftoff.

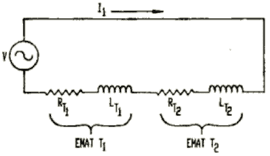
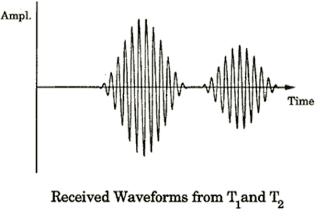
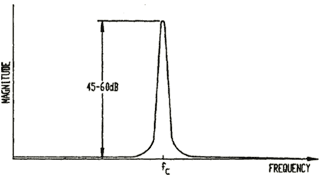
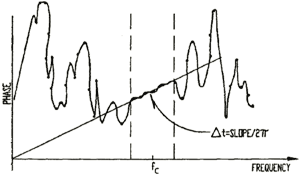
Slope of the phase is determined by linear regression of weighted data points within the signal bandwidth and a weighted y-intercept. The accuracy obtained with this method can exceed one part in one hundred thousand (1:100,000).