Ultrasonic Measurement of Stress

For sheet and plate specimens experiencing applied or residual stress, the principal stresses s_a and s_b may be inferred from orthogonal velocity measurements. The following equation relates ultrasonic velocities to the principal stresses experienced in sheets or plates.

$$2pV_{avg}\cdot [V(\phi^{\circ})-V(\phi^{\circ}+90^{\circ})]=s_a-s_b$$

V_avg is the average shear velocity. It is understood that velocity difference $[V(\phi^{\circ})-V(\phi^{\circ}+90^{\circ})]$ will be maximized when the ultrasonic propagation directions are aligned with principal stress axes. The magnitude of this difference, along with the density and mean velocity can be used to predict the principal stress difference.

It is particularly noteworthy that no acoustoelastic constants or other nonlinear properties of the material are needed for a stress prediction, which distinguishes this approach from other ultrasonic stress measurement techniques. The nonlinear material characteristics have been suppressed by the process of taking the velocity difference.

Measurement Technique

Differential velocity is measured using a T₁-T₂-R fixed array of EMAT transducers at 0° and 90° relative rotational directions depending on device configuration.

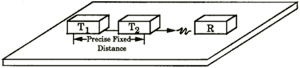
EMAT Driver Frequency: 450-600 kHz (nomioverview_stress.gifnal)
Sampling Period: 100 ns
Time Measurement Accuracy:

• Resolution: 0.05 Ns
• Accuracy required for less than 2 KSI Stress Measurements: Variance 2.47 Ns