Transducer Beam Spread
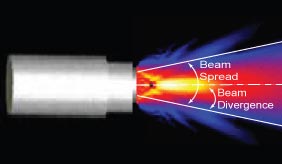 As discussed on the previous page, round transducers are often referred to as piston source transducers because the sound field resembles a cylindrical mass in front of the transducer. However, the energy in the beam does not remain in a cylinder, but instead spreads out as it propagates through the material. The phenomenon is usually referred to as beam spread but is sometimes also referred to as beam divergence or ultrasonic diffraction. It should be noted that there is actually a difference between beam spread and beam divergence. Beam spread is a measure of the whole angle from side to side of the main lobe of the sound beam in the far field. Beam divergence is a measure of the angle from one side of the sound beam to the central axis of the beam in the far field. Therefore, beam spread is twice the beam divergence.
As discussed on the previous page, round transducers are often referred to as piston source transducers because the sound field resembles a cylindrical mass in front of the transducer. However, the energy in the beam does not remain in a cylinder, but instead spreads out as it propagates through the material. The phenomenon is usually referred to as beam spread but is sometimes also referred to as beam divergence or ultrasonic diffraction. It should be noted that there is actually a difference between beam spread and beam divergence. Beam spread is a measure of the whole angle from side to side of the main lobe of the sound beam in the far field. Beam divergence is a measure of the angle from one side of the sound beam to the central axis of the beam in the far field. Therefore, beam spread is twice the beam divergence.
Although beam spread must be considered when performing an ultrasonic inspection, it is important to note that in the far field, or Fraunhofer zone, the maximum sound pressure is always found along the acoustic axis (centerline) of the transducer. Therefore, the strongest reflections are likely to come from the area directly in front of the transducer.
Beam spread occurs because the vibrating particle of the material (through which the wave is traveling) do not always transfer all of their energy in the direction of wave propagation. Recall that waves propagate through the transfer of energy from one particle to another in the medium. If the particles are not directly aligned in the direction of wave propagation, some of the energy will get transferred off at an angle. (Picture what happens when one ball hits another ball slightly off center). In the near field, constructive and destructive wave interference fill the sound field with fluctuation. At the start of the far field, however, the beam strength is always greatest at the center of the beam and diminishes as it spreads outward.
As shown in the applet below, beam spread is largely determined by the frequency and diameter of the transducer. Beam spread is greater when using a low frequency transducer than when using a high frequency transducer. As the diameter of the transducer increases, the beam spread will be reduced.
Beam angle is an important consideration in transducer selection for a couple of reasons. First, beam spread lowers the amplitude of reflections since sound fields are less concentrated and, thereby weaker. Second, beam spread may result in more difficulty in interpreting signals due to reflections from the lateral sides of the test object or other features outside of the inspection area. Characterization of the sound field generated by a transducer is a prerequisite to understanding observed signals.
Numerous codes exist that can be used to standardize the method used for the characterization of beam spread. American Society for Testing and Materials ASTM E-1065, addresses methods for ascertaining beam shapes in Section A6, Measurement of Sound Field Parameters. However, these measurements are limited to immersion probes. In fact, the methods described in E-1065 are primarily concerned with the measurement of beam characteristics in water, and as such are limited to measurements of the compression mode only. Techniques described in E-1065 include pulse-echo using a ball target and hydrophone receiver, which allows the sound field of the probe to be assessed for the entire volume in front of the probe.
For a flat piston source transducer, an approximation of the beam spread may be calculated as a function of the transducer diameter (D), frequency (F), and the sound velocity (V) in the liquid or solid medium. The applet below allows the beam divergence angle (1/2 the beam spread angle) to be calculated. This angle represents a measure from the center of the acoustic axis to the point where the sound pressure has decreased by one half (-6 dB) to the side of the acoustic axis in the far field.
Note: This applet uses the equation:
| Where: | θ = Beam divergence angle from centerline to point where signal is at half strength. |
| V = Sound velocity in the material. (inch/sec or cm/sec)1 | |
| a = Radius of the transducer. (inch or cm)1 | |
| F = Frequency of the transducer. (cycles/second) |
Note 1: Units must be consistent throughout calculation (i.e. inch or cm but not both)
An equal, but perhaps more common version of the formula is:
| Where: | θ = Beam divergence angle from centerline to point where signal is at half strength. |
| V = Sound velocity in the material. (inch/sec or cm/sec) | |
| D = Diameter of the transducer. (inch or cm) | |
| F = Frequency of the transducer. (cycles/second) |