Thompson-Gray Measurement Model
The Thompson-Gray Measurement Model allows the approximate prediction of ultrasonic scattering measurements made through liquid-solid interfaces. Liquid-solid interfaces are common in physical inspection scenarios. The model allows us to make predictions about received ultrasonic signals scattered from various classes of defects. The model predicts an absolute scattering amplitude in the sense that amplitudes are correct and transducer and system characteristics are removed by deconvolution techniques.
Work begun in the early 1980's continues to be refined and has resulted into an increasingly valuable working tool for comparison of ultrasonic theory and experiment. The Thompson-Gray Measurement Model is at the heart of UTSIM (see section 5.4 Ultrasonic Simulation - UTSIM).
The validity of any model rests on how well its predictions agree with experiment. Shown below are three examples taken from the J. Acoust. Soc. Am., 74(4) October 1983 entitled, "A model relating ultrasonic scattering measurements through liquid-solid interfaces to unbounded medium scattering amplitudes."
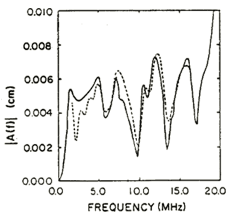
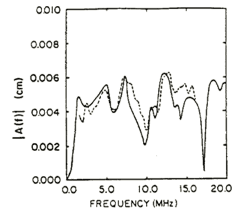
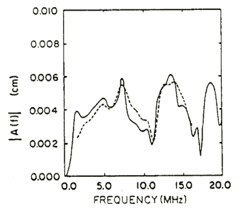
Comparison of theory and experimental magnitude of longitudinal pitch-catch scattering amplitude for a 114 µm radius tin-lead solder sphere in a Lucite cylindrical disk. Illumination was at normal incidence and reception at an 8° angle (15° in the solid) (left), 15.7° angle (30° in the solid) (center), and a 22.5° angle (45° in the solid) (right).
The relationship between scattering data (obtained from ultrasonic experiments in which the waves are excited and detected in a finite measurement geometry) and unbounded medium, farfield scattering amplitudes, forms the basis of an ultrasonic measurement model.
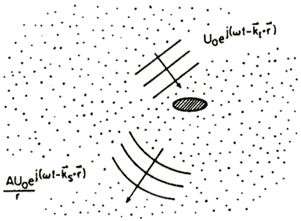
The associated amplitudes are: for the incoming sound waves and for the scattered wave.
For a scatterer in a single fluid medium, a Green's function approach is used to develop an approximate but absolute relationship between these experimental and theoretical cases.
Electromechanical reciprocity relationships are then employed to generalize to a two medium case in which the scatterer is located in an elastic solid which, along with the ultrasonic transducer, is immersed in a fluid medium.
The scattering of elastic waves by a flaw in, an unbounded solid, e.g., a crack, void, or inclusion, is often characterized by a scattering amplitude A which defines the spherically spreading wave scattered into the farfield when the flaw is "illuminated" by a unit amplitude plane wave, as schematically illustrated in the above diagram. However, measurements of scattering are always made with transducers of finite aperture, at finite distances from the scatterer. Furthermore, the transducer is often immersed in a fluid medium and the wave has passed through the liquid-solid interface twice during the measurement.
In principle, complete theoretical scattering solutions can be developed for this more complex scattering situation. However, even the introduction of the liquid-solid interface significantly complicates the elastic wave scattering and further introduction of finite beam effects in an exact manner would generally lead to computational complexity, which would severely restrict the use of the results in the routine interpretation of experiments.
An alternative point of view would be to view the unbounded medium scattering amplitude A as a canonical solution and to develop approximate expressions, which relate this to the solutions for the more complex measurement geometries. This point of view is routinely adopted in studies of the acoustic scattering (e.g. sonar) from various obstacles. In this case, the problem is greatly simplified by the fact that: (a) the fluid medium only supports a single wave type, (b) the waves do not pass through a refracting and mode converting interface, and (c) calibration experiments can be performed with arbitrary relative positions of transducers and reflecting surfaces to eliminate diffraction effects.