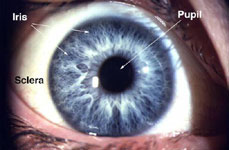
Visual Acuity of the Human Eye
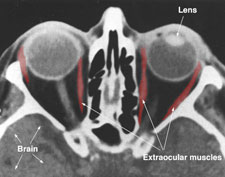
The eye has a visual acuity threshold below which an object will go undetected. This threshold varies from person to person, but as an example, the case of a person with normal 20/20 vision can be considered. As light enters the eye through the pupil, it passes through the lens and is projected on the retina at the back of the eye. Muscles called extraocular muscles, move the eyeball in the orbits and allow the image to be focused on the central retinal or fovea.
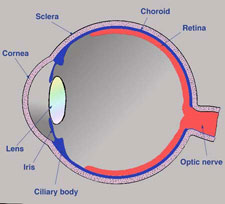
The retina is a mosaic of two basic types of photoreceptors: rods, and cones. Rods are sensitive to blue-green light with peak sensitivity at a wavelength of 498 nm, and are used for vision under dark or dim conditions. There are three types of cones that give us our basic color vision: L-cones (red) with a peak sensitivity of 564 nm, M-cones (green) with a peak sensitivity of 533 nm, and S-cones (blue) with a peak sensitivity of 437 nm.
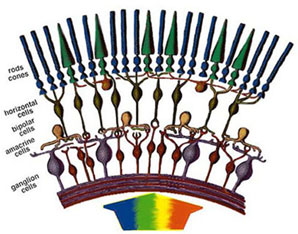
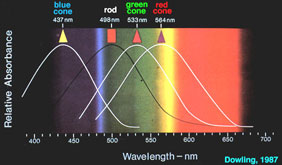
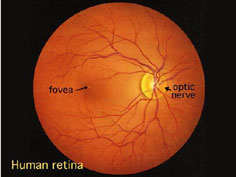
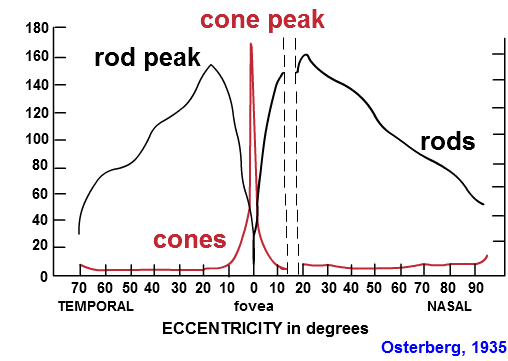
Cones are highly concentrated in a region near the center of the retina called the fovea region. The maximum concentration of cones is roughly 180,000 per square mm in the fovea region and this density decreases rapidly outside of the fovea to a value of less than 5,000 per square mm. Note the blind spot caused by the optic nerve which is void of any photoreceptors.
The standard definition of normal visual acuity (20/20 vision) is the ability to resolve a spatial pattern separated by a visual angle of one minute of arc. Since one degree contains sixty minutes, a visual angle of one minute of arc is 1/60 of a degree. The spatial resolution limit is derived from the fact that one degree of a scene is projected across 288 µm of the retina by the eye's lens.
In this 288 µm, there are 120 color sensing cone cells packed. Thus, if more than 120 alternating white and black lines are crowded side-by-side in a single degree of viewing space, they will appear as a single gray mass to the human eye. With a little trigonometry, it is possible to calculate the resolution of the eye at a specific distance away from the lens of the eye.
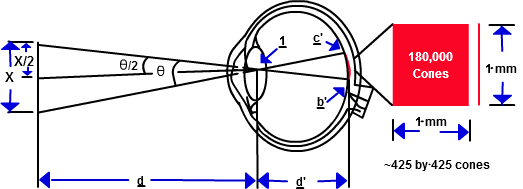
For the case of normal visual acuity the angle Theta is 1/60 of a degree. By bisecting this angle we have a right triangle with angle Theta/2 that is 1/120 of a degree. Using this right triangle it is easy to calculate the distance X/2 for a given distance d.
When visually inspecting an object for a defect such as a crack, the distance (d) might be around 12 inches. This would be a comfortable viewing distance. At 12 inches, the normal visual acuity of the human eye is 0.00349 inch. What this means is that if you had alternating black and white lines that were all 0.00349 inch wide, it would appear to most people as a mass of solid gray.