Impedance Calculation
|
and Where: = Complex Impedance (ohm) = Amplitude of the Impedence (ohm) R = Resistance (ohm) XL = Inductive Reactance(ohm) Xc = Capacitive Reactance(ohm) |
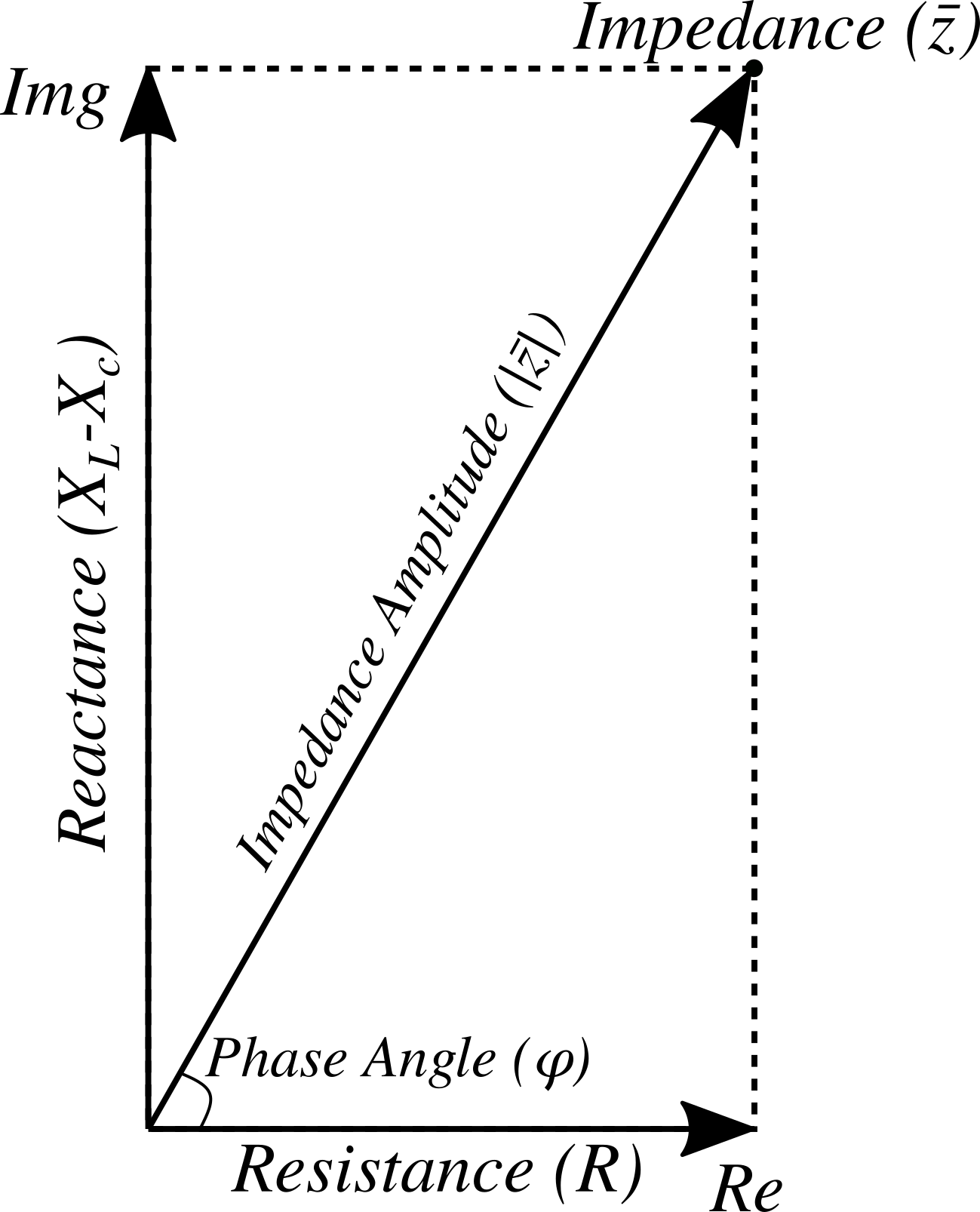
Electrical Impedance (), is the total opposition that a circuit presents to alternating current. Impedance is measured in ohms () and may include resistance (R), inductive reactance (XL), and capacitive reactance (Xc). Capacitive reactance is usually not present in eddy current testing so this term is not included the equation.
The total impedance is not simply the algebraic sum of resistance and inductive reactance. Since the inductive reactance is 90 degrees out of phase with the resistance and, therefore, their maximum values occur at different times, vector addition must be used to calculate impedance. This is illustrated in the image to the right.
If the amount of resistance is represented by the length of the horizontal line and the amount of inductive reactance is represented by the length of the vertical line; then, the amount of impedance is represented by the length of the diagonal line. Since the lines form a right triangle, the Pythagorean theorem can be used to find the length (value) of the impedance line.
The Pythagorean theorem is written:
For this application the variable, a is equal to resistance, b is equal to reactance, and c is equal to the impedance. So, the equation becomes:
As stated earlier, Xc is taken to be zero, so
Example Calculation:
Calculate the impedance when the resistance is 0.6 ohms and the inductive reactance is 0.4 ohms.
Simply plug in the values and solve for .