Eddy Current Inspection Formulas

$$I= \frac{V}{Z}$$

$$$$Where:

I = Current (ampere or amp)

V = Voltage (volt)

Z = Impedance (ohm)

Learn more about Ohm's Law.

$$\bar{Z}=R+X_{L}-X_{c}$$

and

$$\vert \bar{Z}\vert=\sqrt{R^{2}+(X_{L}-X_{c})^{2}}$$

$$$$Where:

$\bar{Z}$ = Complex Impedance (ohm)

$\vert \bar{Z}\vert$ = Magnitude of the Impedance (ohm)

R = Resistance (ohm)

X_L = Inductive Reactance(ohm)

X_c = Capacitive Reactance(ohm)

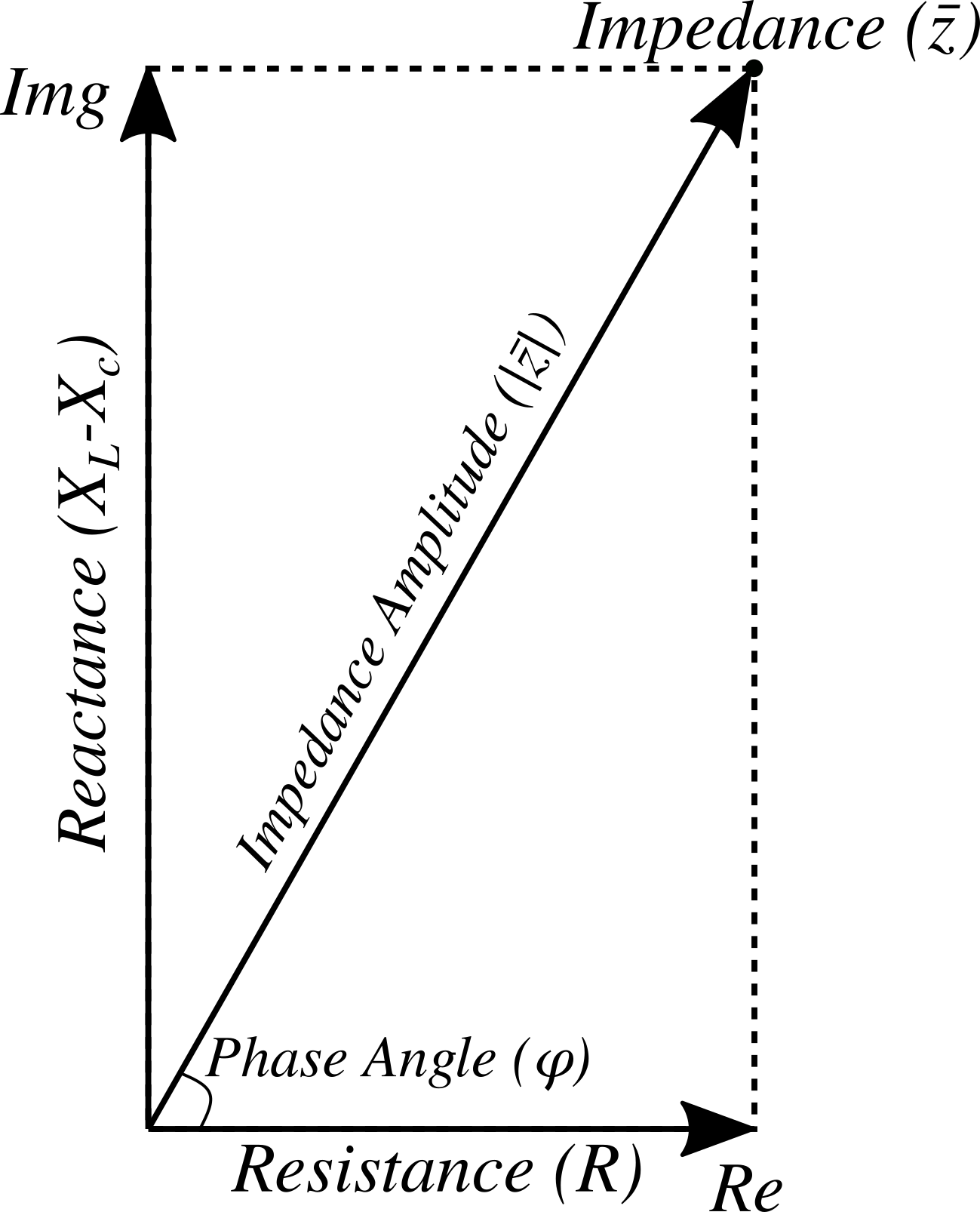
Electrical impedance ($\bar{Z}$), is the total opposition that a circuit presents to alternating current. Impedance is measured in ohms ($\Omega$) and may include resistance (R), inductive reactance (X_L), and capacitive reactance (X_c). Capacitive reactance is usually not present in eddy current testing so this term is not included the equation.

The total impedance is not simply the algebraic sum of resistance and inductive reactance. Since the inductive reactance is 90 degrees out of phase with the resistance and, therefore, their maximum values occur at different times, vector addition must be used to calculate impedance. This is illustrated in the image to the right.

If the amount of resistance is represented by the length of the horizontal line and the amount of inductive reactance is represented by the length of the vertical line; then, the amount of impedance is represented by the length of the diagonal line. Since the lines form a right triangle, the Pythagorean theorem can be used to find the length (value) of the impedance line.

The Pythagorean theorem is written: $$c^{2}=a^{2}+b^{2}$$

For this application the variable, a is equal to resistance, b is equal to reactance, and c is equal to the impedance. So, the equation becomes:

$$\bar{Z}^{2}=R^{2}+(X_{L}-X_{c})^{2}$$

As stated earlier, Xc is taken to be zero, so

$$\vert \bar{Z}\vert=\sqrt{R^{2}+X_{L}^{2}}$$

Example Calculation:

Calculate the impedance when the resistance is 0.6 ohms and the inductive reactance is 0.4 ohms.

Simply plug in the values and solve for $\vert \bar{Z}\vert$.

$$\vert \bar{Z}\vert=\sqrt{.6^{2}+.4^{2}}$$

$$\vert \bar{Z}\vert=\sqrt{.36+.16}$$

$$\vert \bar{Z}\vert=\sqrt{.52}$$

$$\vert \bar{Z}\vert=.72$$

$$\tan\phi= \frac{X}{R}$$

$$$$Where:

ϕ = Phase Angle (radians)

X = Reactance (ohm)

R = Resistance (ohm)

Although both the current and the voltage oscillate sinusoidally in an AC circuit they do not necessarily rise and fall simultaneously with each other. The current and voltage will oscillate with the same frequency but they will only be in-phase if the circuit contains only resistance (or if the circuit is in resonance). In this case, when the voltage is at it's maximum, the current will also be at its maximum, and the impedance purely real. However, when a circuit also contains reactance, the voltage and the current shift out of phase. This shift occurs because when the change in current is highest, it will create the greatest amount of inductive reactance (X_L)in the circuit. While the capacitive reactance X_c also contributes, it is insignificant during eddy current tests compared to X_L. This inductive reactance is responsible for the voltage across the inductor. See these pages for a better explanation of inductive reactance and phase shift.

The angle by which the sine curve of the voltage in a circuit leads or lags the sine curve of the current in the circuit is called the phase angle (ϕ). If f is positive the voltage leads the current. The phase angle can be determined from the components of impedance that make up the circuit. The phase angle can be calculated from the simple trigonometric relationship between the inductive reactance and the resistance on the impedance plane. It can also be seen from the impedance plane that when the total impedance and the phase angle are known, the individual components of the impedance (inductive reactance and resistance) can be calculated. This is what occurs most often in practice. Most instruments measure the total impedance and the phase angle between the drive current and the voltage across the coil. This information can then be used to calculate the resistance and inductive reactance components of the signal if needed.

Magnetic permeability:

$$\mu= \frac{B}{H}$$

Where:

$\mu$ = Magnetic Permeability (Henries/meter)

B = Magnetic Flux Density (Tesla)

H = Magnetizing Force (Am/meter)

Relative Magnetic Permeability:

$$\mu_{r}= \frac{\mu}{\mu_{0}}$$

Where:

μ_r = Relative Magnetic Permeability (dimensionless)

μ = Any Given Magnetic Permeability (H/m)

μ_o = Magnetic Permeability in Free Space (H/m), which is 1.257 x 10^-6 H/m

Magnetic permeability is the ease with which a material can be magnetized. It is a constant of proportionality that exists between magnetic induction and magnetic field intensity. This constant is equal to approximately 4π x10^-7 henry per meter or 1.257 x 10^-6 H/m in free space (a vacuum). In other materials permeability can be much different, often substantially greater than the free-space value, which is symbolized µ_o.

In engineering applications, permeability is often expressed in relative, rather than in absolute, terms. If µ_o represents the permeability of free space and µ represents the permeability of the substance in question (also specified in henrys per meter), then the relative permeability, µ_r, is given by the equation above. Relative permeability is dimensionless since it is the ratio of two permeability values expressed in the same units.

Examples:

Example 1

What is the relative permeability of a material with an absolute permeability of 5.63x10^-5H/m?

Simply plug the materials permeability and the free space permeability values in the equation and solve.

$$\mu_{r}= \frac{\mu}{\mu_{0}}$$

$$\mu_{r}=\frac{5.63\times10^{-5}}{1.257 \times 10^{-6}}$$

$$\mu_{r}=44.78$$

Example 2

What is the absolute permeability of a materials with a relative permeability of 1.05

Given the equation and the permeability of free space (µ_o) of 1.257x10^-6 H/mm Rearranging this equation to solve for absolute permeability results in:

$$\mu_{r}= \frac{\mu}{\mu_{0}}$$

$$\mu=\mu_{r}\mu_{0}$$

Plugging the given values into the equation produces an absolute permeability value.

$$\mu=1.05\times1.257\times10^{-6}$$

$$\mu=1.32\times10^{-6}$$

$$\sigma= \frac{1}{\rho}$$

Where:

σ= Electrical Conductivity Siemens/m

ρ= Electrical Resistivity (ohm-m)

More on Resistance and Conductivity

When resistivity is known:

$$\sigma_{\text{$$

Where:

σ_%IACS = Electrical Conductivity (%IACS)

ρ= Electrical Resistivity (μohm-cm)

When conductivity in S/m or μS/cm is known:

$$\sigma_{\text{$$

or

$$\sigma_{\text{$$

Where:

σ_%IACS = Electrical Conductivity (%IACS)

σ_S/m = Electrical Conductivity (Siemens/meter)

σ_μS/cm = Electrical Conductivity (μSiemens/cm)

The SI derived unit for conductivity is the Siemen per meter, but conductivity values are often reported as %IACS. IACS is an acronym for International Annealed Copper Standard, which is the material used to make traditional copper electrical wire. The conductivity of the annealed copper is 5.8 x 10⁷S/m and copper is defined to be 100 %IACS at 20°C. All other conductivity values are related back to this conductivity of annealed copper. Therefore, iron with a conductivity value of 1.044 x 10⁷ S/m, has a conductivity of approximately 18% of that of annealed copper and this is reported as 18 %IACS. Conductivity values in Siemen/meter can be converted to %IACS by dividing the conductivity value by 5.8 x 10⁷S/m (the conductivity of annealed copper) and multiplying by 100.

Often reference materials contain the "172.41" term as shown in the second equation. This term is simply arrived at by taking the inverse of the 5.8 x 10⁷S/m copper conductivity value. This make it very easy to convert to %IACS when conductivity values are reported in μSiemens/cm because the value is simply multiplied by 172.41.

Also, conductivity and resistivity are inversely proportional. A conductor with a conductivity of 58 MegaSiemens per meter (MS/m) will have a resistivity of 1/58 ohm-meter. To convert resistivity values to %IACS conductivity values, simply divide 172.41 by the resistivity value in μohm-cm.

An interesting side note is that commercially pure copper products now often have IACS conductivity values greater than 100% because processing techniques have improved since the adoption of the standard in 1913 and more impurities can now be removed from the metal.

Material Thickness Requirement for Resistivity or Conductivity Measurement

When measuring resistivity or conductivity, the thickness of the material should be at least 3 times the depth of penetration to minimize material thickness effects

$$t\geq3\delta$$

Where:

t = Material Thickness

δ= Standard Depth of Penetration

$$J_{x}=J_{0}e^{\frac{-x}{\delta}}$$

Where:

J_x = Current Density (amps/m²)

J_o = Current Density at Surface (amps/m²)

e = Base Natural Log = 2.71828

x = Distance Below Surface

δ = Standard Depth of Penetration

Learn more about eddy current density and skin depth.

Standard Depth when Electrical Conductivity (S/m) is Known

$$\delta\approx \frac{1}{\sqrt{\pi f\mu\sigma}}$$

Where:

δ = Standard Depth of Penetration (m)

π = 3.14

f = Test Frequency (Hz)

μ = Magnetic Permeability (H/m) (1.257 x 10^-6 H/m for nonmagnetic materials)

σ = Electrical Conductivity (Siemens/m)

Eddy currents are more concentrated at the surface and decrease in intensity with distance below the surface of the metal. This effect is known as the "skin effect." The depth at which eddy current density has decreased to 1/e, or about 37% of the surface density, is called the standard depth of penetration (δ). Although eddy currents penetrate deeper than one standard depth of penetration, they decrease rapidly with depth. At two standard depths of penetration (2δ), the eddy current density has decreased to 1/e squared or 13.5% of the surface density. At three depths (3δ), the eddy current density is down to only 5% of the surface density.

The depth of penetration is dependent of test drive frequency, the test material's conductivity and magnetic permeability. The depth of penetration decreases with increasing frequency, conductivity and permeability. It is important to know the standard depth of penetration because for some testing (like flaw detection) the inspection should be conducted at a frequency that places the depth of any likely flaws at 1d or less where eddy currents are strong. When making conductivity tests, the sample should be at least 3δ thick so that changes in the thickness of the sample do not affect the measurements. When electrical conductivity in %IACS and permeability in H/mm are known, the standard depth of penetration can be calculated using the equation to the right.

Working with this Equation

In many places, magnetic permeability is presented as relative permeability. The relative magnetic permeability is defined as the permeability of a material relative to the permeability of free space (vacuum) which equals roughly 4π x10^-7 H/m. Therefore, it may be necessary to multiply the given relative permeability value by 4π x10^-7 H/m or 1.257 x10^-6 H/m to get the absolute permeability value which is needed in this equation. Since the magnetic permeability of nonmagnetic materials is close to that of free space, the free space value is commonly used.

Also, electrical conductivity values are often expressed as a percent of the conductive of pure, annealed copper measured at 25^oC. At this temperature, the conductivity of pure copper is 5.8 x10⁷ siemens/meter or 100 %IACS. IACS is an acronym for International Annealed Copper Standard. A material that has a conductivity of 3.2x10⁷ siemens/meter can be also be expressed as 57 %IACS and visa versa.

Examples

Example 1

What is the standard depth of penetration when performing an eddy current inspection on a piece of 304 Corrosion Resistant Steel? The material has a relative permeability of 1.05 and a conductivity of 2.5 %IACS. The frequency used to drive the eddy current probe is 50 kHz.

First, since relative permeability is given, it must be converted to an absolute permeability value. Given the equation and the permeability of free space (u₀) of 1.257x10^-6 H/m Rearranging this equation to solve for absolute permeability results in: $$\mu_{r}=\frac{\mu}{\mu_{0}}$$ $$\mu=\mu_{r}\mu_{0}$$

Plugging the given values into the equation produces an absolute permeability value. $$\mu=(1.05)(1.257\times10^{-6})$$ $$\mu=1.32\times10^{-6}\text{ H/m}$$

Since conductivity is expressed in %IACS, it must be converted to siemens/meter. $$\text{$$ $$(\text{$$ $$(0.025)(5.8\times 10^{7})=\sigma_{material}$$ $$1.45\times 10^{6}\text{ Siemens/m}=\sigma_{material}$$

Then plug-in the values and solve the equation. $$\delta=\frac{1}{\sqrt{\pi f\mu\sigma}}$$ $$\delta=\frac{1}{\sqrt{\pi \times 50,000\times (1.32\times 10^{-6})\times (1.45\times10^{6})}}$$ $$\delta=.0018\text{ meters}$$ or $$\delta=1.8\text{ mm}$$

Tip: You may have noticed that there is a term with 10^-6 and a term with 10⁶ in the denominator of the equation and they can be canceled to make the equation easier to solve.

Example 2

Determine the frequency needed to achieve a depth of penetration of 2mm in 7075-T76 aluminum plate.

Aluminum is nonmagnetic so its relative permeability is one and its permeability is the same as that of free space (1.257x10^-6 H/mm). With a measurement or from the Electrical Conductivity and Resistivity Property Tables, determine the conductivity value for the material. The value given is 38.5 %IACS is given in the table so it must be converted to Siemens/m. $$\text{$$ $$(\text{$$ $$(0.385)(5.8\times 10^{7})=\sigma_{material}$$ $$2.23\times 10^{7}\text{ Siemens/m}=\sigma_{material}$$

The depth of penetration equation must be rearranged to solve for frequency (f). $$\delta=\frac{1}{\sqrt{\pi f\mu\sigma}}$$

First square both sides to eliminate the square root. $$\delta^{2}=\frac{1^{2}}{\pi f\mu\sigma}$$

Multiply both sides by πfμσ $$\delta^{2}\pi f\mu\sigma=1$$

Then divide both sides by to isolate δ²πμσ $$f=\frac{1}{\delta^{2}\pi \mu\sigma}$$

Plug in the known values and solve. Notice that the depth of penetration (2mm) had to be converted to meters (0.002m) because δ must be in meters for this equation to work. $$f=\frac{1}{(.002)^{2}\pi (1.256\times 10^{-6})(2.23\times10^{7})}$$ $$f=2,841 \text{ Hz}$$ $$f=2.8 \text{ kHz}$$

Standard Depth when Electrical Conductivity (%IACS) is Known

In mm: $$\delta_{mm}\approx \frac{661}{\sqrt{f\mu_{r}\sigma}}$$

In Inches: $$\delta_{inch}\approx \frac{26}{\sqrt{f\mu_{r}\sigma}}$$

Where:

δ = Standard Depth of Penetration (mm or in)

f = Test Frequency (Hz)

μ_r = Relative Magnetic Permeability (dimensionless)

σ = Electrical Conductivity (%IACS)

Examples

Example 1

What is the standard depth of penetration when performing an eddy current inspection on a piece of 304 Corrosion Resistant Steel? The material has a relative permeability of 1.05 and a conductivity of 2.5% IACS. The frequency used to drive the eddy current probe is 50 kHz.

Simply plug-in the known values and solve the equation. $$\delta \approx \frac{661}{\sqrt{f\mu_{r}\sigma}}$$ $$\delta \approx \frac{661}{\sqrt{(50,000)(1.05)(2.5)}}$$ $$\delta \approx 1.8\text{ mm}$$

Example 2

Determine the frequency needed to achieve a depth of penetration of 2mm in 7075-T76 aluminum plate.

Aluminum is nonmagnetic so its relative permeability is one. With a measurement or from the Electrical Conductivity and Resistivity Property Tables, determine the conductivity value for the material. The value given in the table is 38.5% IACS. $$\delta \approx \frac{661}{\sqrt{f\mu_{r}\sigma}}$$

The depth of penetration equation must be rearranged to solve for frequency (f). Start by squaring both sides to clear the square root. $$\delta^{2} \approx \left(\frac{661}{\sqrt{f\mu_{r}\sigma}}\right)^{2}$$ $$\delta^{2} \approx \frac{661^{2}}{f\mu_{r}\sigma}$$

Then solve for frequency. $$f \approx \frac{436,921}{\delta^{2}\mu_{r}\sigma}$$

Plug in the known values and solve. $$f \approx \frac{436,921}{(2^{2})(1)(38.5)}$$ $$f \approx 2.8 \text{kHz}$$

Standard Depth when Electrical Resistivity (μohm-cm) is Known

In mm: $$\delta_{mm}\approx 50 \sqrt{\frac{\rho}{f\mu_{r}}}$$

In inches: $$\delta_{inch}\approx 1.98 \sqrt{\frac{\rho}{f\mu_{r}}}$$

Where:

δ = Standard Depth of Penetration (mm or in)

ρ = Electrical Resistivity (μohm-cm)

f = Test Frequency (Hz)

μ_r = Relative Magnetic Permeability (dimensionless)

Eddy currents are more concentrated at the surface and decrease in intensity with distance below the surface of the metal. This effect is known as the "skin effect." The depth at which eddy current density has decreased to 1/e, or about 37% of the surface density, is called the standard depth of penetration (δ). Although eddy currents penetrate deeper than one standard depth of penetration, they decrease rapidly with depth. At two standard depths of penetration (2δ), the eddy current density has decreased to 1/e squared or 13.5% of the surface density. At three depths (3δ), the eddy current density is down to only 5% of the surface density.

The depth of penetration is dependent of test drive frequency, the test material's conductivity and magnetic permeability. The depth of penetration decreases with increasing frequency, conductivity and permeability. It is important to know the standard depth of penetration because for some testing (like flaw detection) the inspection should be conducted at a frequency that places the depth of any likely flaws at 1δ or less where eddy currents are strong. When making conductivity tests, the sample should be at least 3δ thick so that changes in the thickness of the sample do not affect the measurements. When electrical conductivity in % IACS and permeability in H/mm are known, the standard depth of penetration can be calculated using the equation to the right.

Working with this Equation

In many places, magnetic permeability is presented as relative permeability. The relative magnetic permeability is defined as the permeability of a material relative to the permeability of free space (vacuum) which equals roughly 4π x10^-7 H/m. Since the magnetic permeability of nonmagnetic materials is close to that of free space, the value of one is used as the relative permeability.

Example 1

What is the standard depth of penetration when performing an eddy current inspection on a piece of 304 Corrosion Resistant Steel? The material has a relative permeability of 1.05 and a conductivity of 2.5% IACS. The frequency used to drive the eddy current probe is 50 kHz.

Since conductivity in %IACS is known, it must be converted to resistivity in μohm-cm. $$\sigma=\frac{172.41}{\rho}$$ $$\rho=\frac{172.41}{\sigma}$$ $$\rho=\frac{172.41}{2.5}$$ $$\rho=68.96\text{ }\mu\text{ohm-cm}$$

Then plug-in the values and solve the equation. $$\delta_{mm}= 50 \sqrt{\frac{\rho}{f\mu_{r}}}$$ $$\delta_{mm}= 50 \sqrt{\frac{68.96}{(50,000)(1.05)}}$$ $$\delta_{mm}= 1.8\text{ mm}$$

Example 2

Determine the frequency needed to achieve a depth of penetration of 2mm in 7075-T76 aluminum plate.

Aluminum is nonmagnetic so its relative permeability is one. With a measurement or from the Electrical Conductivity and Resistivity Property Tables, determine the resistivity value for the material. The value given in the table is 4.48x10^-8 ohm-meters, which is 4.48 μohm-cm.

The depth of penetration equation must be rearranged to solve for frequency (f). $$\delta= 50 \sqrt{\frac{\rho}{f\mu_{r}}}$$ $$\delta^{2}= 50^{2} \frac{\rho}{f\mu_{r}}$$ $$f=\frac{50^{2}\rho}{\delta^{2}\mu_{r}}$$

Plug in the known values and solve. $$f=\frac{50^{2}(4.48)}{(2)^{2}(1)}$$ $$f=2,800\text{ Hz}$$ or $$f=2.8\text{ kHz}$$

Standard Depth of Penetration and Phase Angle

Std. Depth	Relative Strength of EC	Phase Lag
0	e0=100%	0 rad = 0o
δ	e-1=37%	1 rad = 57.3o
2δ	e-2=14%	2 rad = 114.6 o
3δ	e-3=5%	3 rad = 171.9 o
4δ	e-4=2%	4 rad = 229.2 o
5δ	e-5=0.7%	5 rad = 286.5 o

In Radians $$\theta=\frac{x}{\delta}$$

In Degrees: $$\theta=\frac{x}{\delta}\times57.3$$

Where:

θ = Phase Lag (Rad or Degrees)

x = Distance Below Surface (in or mm)

δ = Standard Depth of Penetration (in or mm)

Phase lag is a parameter of the eddy current signal that makes it possible to obtain information about the depth of a defect within a material. Phase lag is the shift in time between the eddy current response from a disruption on the surface and a disruption at some distance below the surface. Phase lag can be calculated using the equations to the right. The second equation simply converts radians to degrees by multiplying by 180/π or 57.3.

The phase lag calculated with these equations should be about 1/2 the phase rotation seen between the liftoff signal and a defect signal on an impedance plane instrument. Therefore, choosing a frequency that results in a standard depth of penetration of 1.25 times the expected depth of the defect will produce a phase lag of 45^o and this should appear as a 90^o separation between the liftoff and defect signals. $$\theta=\frac{x}{\delta}\times57.3$$ $$\theta=\frac{(1)}{(1.25)}\times57.3$$ $$\theta\approx45^{o}$$ $$2\theta\approx90^{o}$$

The phase lag angle is useful for estimating the distance below the surface of discontinuities that concentrated at a specific depth. Discontinuities such as a crack must be divided into sections along its length and a weighted average determined for phase and amplitude at each position below the surface. For more information see the page explaining phase lag.

Phase Lag when Electrical Conductivity (S/m) is Known

$$\theta=57.3x\sqrt{\pi f\mu_{r}\sigma}$$

Where:

θ = Phase Lag (degrees)

x = Distance Below Surface (m)

π = 3.14

f = Test Frequency (Hz)

μ_r = Relative Magnetic Permeability

σ = Electrical Conductivity (Siemens/m)

Phase Lag when Electrical Conductivity (%IACS) is Known

In mm: $$\theta\approx\frac{x\sqrt{f\mu_{r}\sigma}}{11.54}$$ 

In inches: $$\theta\approx2.2x\sqrt{f\mu_{r}\sigma}$$

Where:

θ = Phase Lag (degrees)

x = Distance Below Surface (mm)

f = Test Frequency (Hz)

μ_r = Relative Magnetic Permeability (dimensionless)

σ = Electrical Conductivity (%IACS)

Phase Lag when Resistivity is Known

When electrical resistivity (μohm-cm) is known.

In mm: $$\theta\approx1.15x\sqrt{\frac{f\mu_{r}}{\rho}}$$

In inches: $$\theta\approx28.94x\sqrt{\frac{f\mu_{r}}{\rho}}$$

Where:

θ = Phase Lag (degrees)

x = Distance Below Surface (inch)

ρ = Electrical Resistivity (μohm-cm)

f = Test Frequency (Hz)

μ_r = Relative Magnetic Permeability (dimensionless)

Frequency Selection for Thickness Measurement of Thin Materials

Selecting a frequency that produces a standard depth of penetration that exceeds the material thickness by 25% will produce a phase angle of approximately 90o between the liftoff signal and the material thickness change signal.

1.25t=δ or t=0.8δ

Frequency Selection for Flaw Detection and Nonconductive Coating Thickness Measurements

Defect Detection

A test frequency that puts the standard depth of penetration at about the expected depth of the defect will provide good phase separation between the defect and liftoff signals.

Set δ= Defect Depth

Nonconductive Coating Thickness Measurement

To minimize effects from the base metal the highest practical frequency should be used.