Controlling Radiation Exposure
When working with radiation, there is a concern for two types of exposure: acute and chronic. An acute exposure is a single accidental exposure to a high dose of radiation during a short period of time. An acute exposure has the potential for producing both nonstochastic and stochastic effects. Chronic exposure, which is also sometimes called "continuous exposure," is long-term, low level overexposure. Chronic exposure may result in stochastic health effects and is likely to be the result of improper or inadequate protective measures.
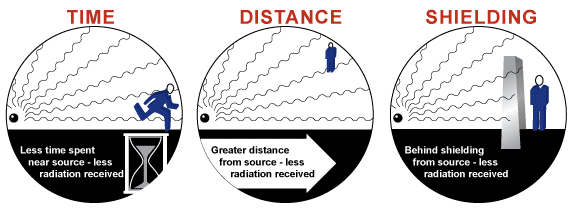
The three basic ways of controlling exposure to harmful radiation are: 1) limiting the time spent near a source of radiation, 2) increasing the distance away from the source, 3) and using shielding to stop or reduce the level of radiation.
Time
The radiation dose is directly proportional to the time spent in the radiation. Therefore, a person should not stay near a source of radiation any longer than necessary. If a survey meter reads 4 mR/h at a particular location, a total dose of 4mr will be received if a person remains at that location for one hour. In a two hour span of time, a dose of 8 mR would be received. The following equation can be used to make a simple calculation to determine the dose that will be or has been received in a radiation area.
Dose = Dose Rate x Time
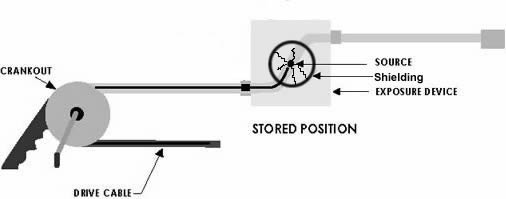
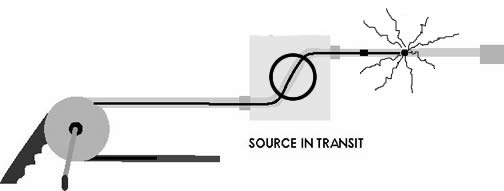
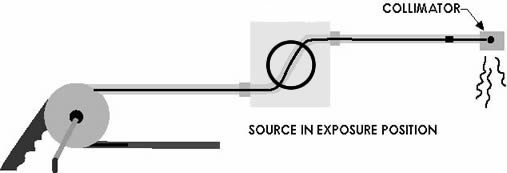
When using a gamma camera, it is important to get the source from the shielded camera to the collimator as quickly as possible to limit the time of exposure to the unshielded source. Devices that shield radiation in some directions but allow it pass in one or more other directions are known as collimators. This is illustrated in the images at the bottom of this page.
Distance
 Increasing distance from the source of radiation will reduce the amount of radiation received. As radiation travels from the source, it spreads out becoming less intense. This is analogous to standing near a fire. The closer a person stands to the fire, the more intense the heat feels from the fire. This phenomenon can be expressed by an equation known as the inverse square law, which states that as the radiation travels out from the source, the dosage decreases inversely with the square of the distance.
Increasing distance from the source of radiation will reduce the amount of radiation received. As radiation travels from the source, it spreads out becoming less intense. This is analogous to standing near a fire. The closer a person stands to the fire, the more intense the heat feels from the fire. This phenomenon can be expressed by an equation known as the inverse square law, which states that as the radiation travels out from the source, the dosage decreases inversely with the square of the distance.
Inverse Square Law:
Shielding
The third way to reduce exposure to radiation is to place something between the radiographer and the source of radiation. In general, the more dense the material the more shielding it will provide. The most effective shielding is provided by depleted uranium metal. It is used primarily in gamma ray cameras like the one shown below. The circle of dark material in the plastic see-through camera (below right) would actually be a sphere of depleted uranium in a real gamma ray camera. Depleted uranium and other heavy metals, like tungsten, are very effective in shielding radiation because their tightly packed atoms make it hard for radiation to move through the material without interacting with the atoms. Lead and concrete are the most commonly used radiation shielding materials primarily because they are easy to work with and are readily available materials. Concrete is commonly used in the construction of radiation vaults. Some vaults will also be lined with lead sheeting to help reduce the radiation to acceptable levels on the outside.